科普八度、十二度

本文是一次上課學生難理解八度、十二度協調等抽象問題。幸好有現代科技把這些抽象玄學數據化。

今次任務是從D4調D3. 為方便理解，各位請先理解這幅圖和一點背景知識：

Partial:/泛音/分音：每彈一個鍵，同時震出一系列有關連的音頻。這些泛音的完美理論關係是最低次，第一分音(1st partial)的倍頻 ＝第二分音(2nd partial)；第一分音 X 3 =第三分音(3rd partial)⋯⋯。

從這幅圖見到第分音293.45 x 2 = 586.9 > 586.4 ???
這種現象稱為失諧/不協和性/inharmonicity(ih)。實測數據較理論數據小，是負ih。

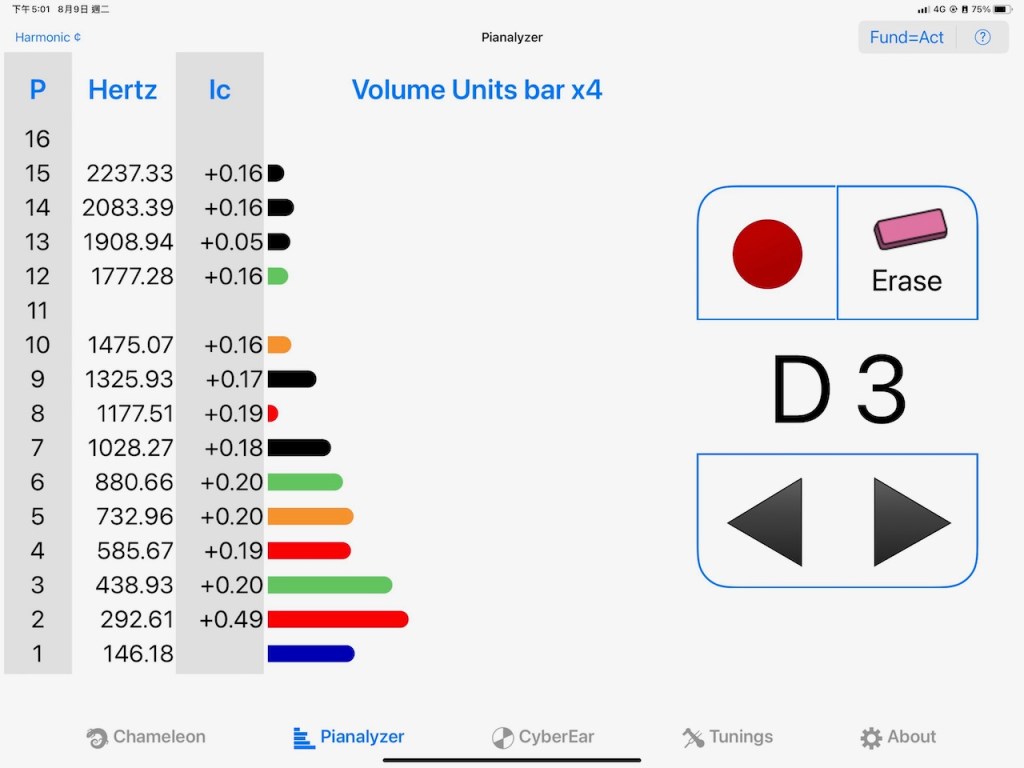
八度是否beatless, 用聽覺調，各分音的拍音可以互相抵消，數據上不完整但聽感上零拍頻。那麼有機會把八度調到“平”：頻率比例剛好是啊2:1? 因聽覺調音是聽泛音之間共鳴，只要有失諧，就不可能調出2:1頻率比例。

八度風格：指的是八度拉伸問題，這對八度從數據上分析是6:3， 即是D3的第6分音(880.66hz)對D4的第三分音(880.93hz)。這可以稱泛音配對/partial matching / coincident partials. 中音區域聽覺調零拍頻八度通常是4:2 和 6:3之間。

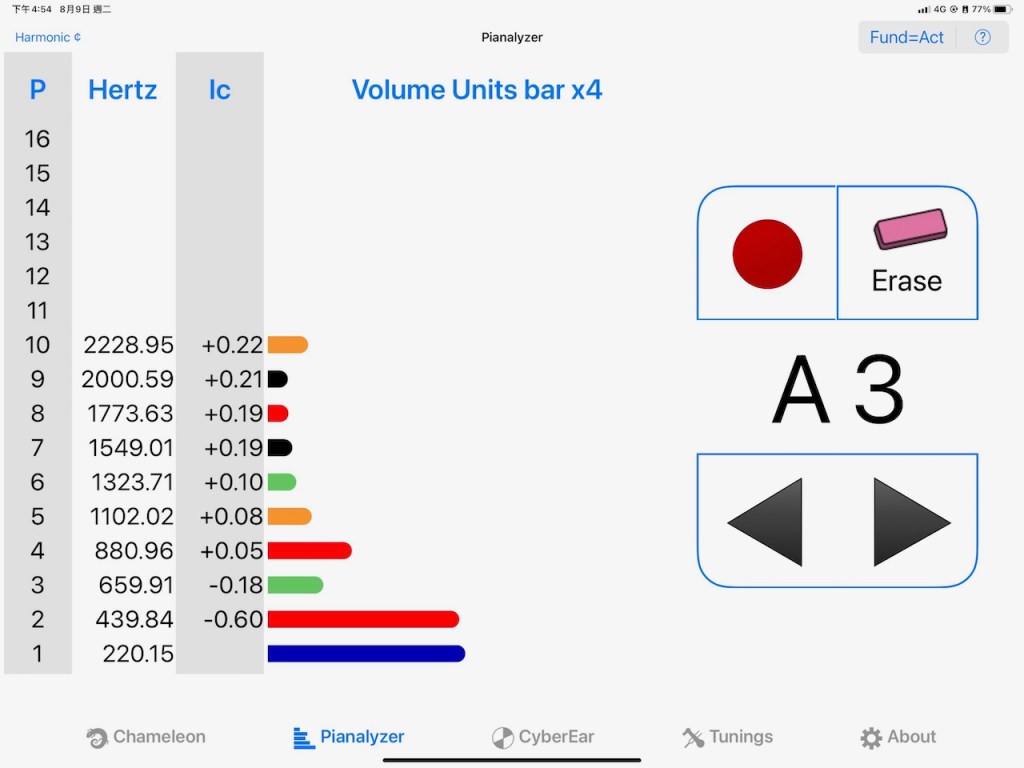
D3-A3這對五度音程，按照3:2風格是闊了，把D3第三分䇎調高些小調到439.84hz就生成一個完美五度。按6:4計，接近一個完美五度。怎麼五度不是要調窄？十二平均律五度理論上要窄二音分，有失諧問題，而這個是向外擴展的八度，要平衡其它音程，理論暫時放下。

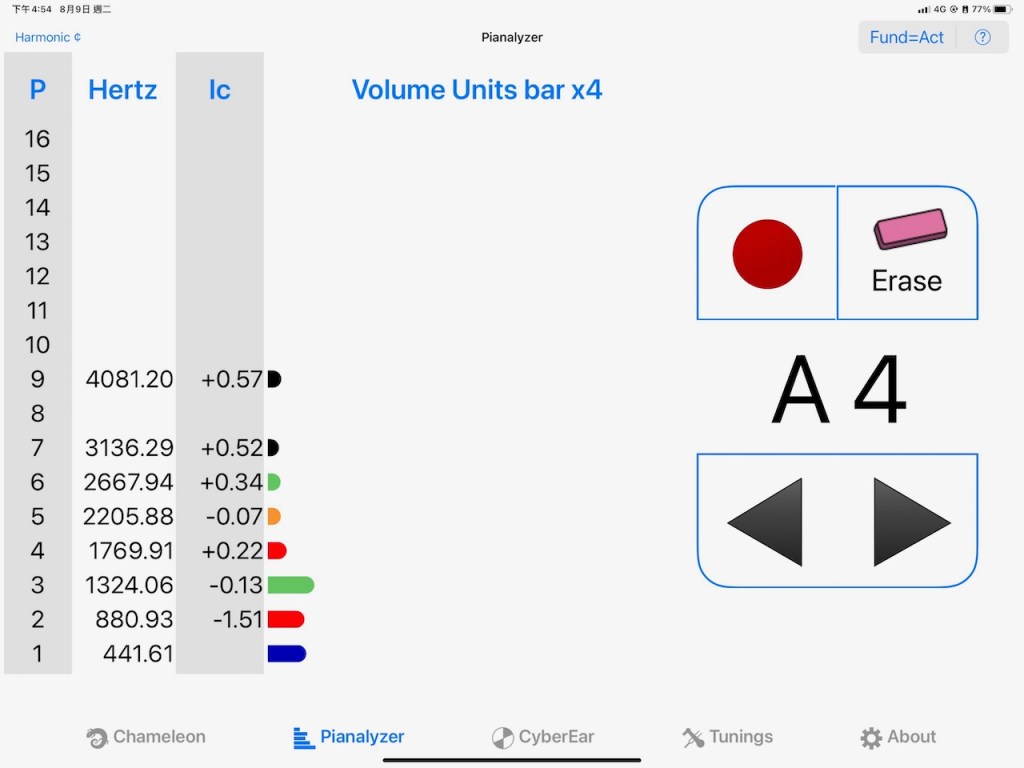
D3-A4是否純十二度？以3:1計，D3第三分音要調高2.68hz；按照6:2計算，也算是完美十二度。

鋼琴音準問題除平均律要求五度調窄些小解決畢氏音差問題(pythagorean comma)問題，還要處理失諧問題。近來興起的純十二度風格，對廣闊音程和音共鳴十分友善。總之一包：鋼琴音準是一個妥協問題。